船体の形状最適化
船舶の産業は、持続可能性と効率性の追求において新たな地平を切り拓いており、この興味深い旅路の中で、船体形状最適化はまさに先駆的な役割を果たしています。
船体形状最適化は、数値モデリングと先端技術を駆使して、船舶の抵抗を最小限に抑え、燃料効率を最適化し、さらには環境に優しい設計を可能にします。
本記事では、最適化プラットフォームAIPODによる船体形状最適化に焦点を当てつつ、AIPODが持つBound-break機能を活用した最適化計算について紹介します。
最適化計算条件について
このケースでは、設計変数が6つ、制約条件が2つの船体をベースとして最適化を行います。
目的関数は、抵抗係数の最小化であり、他の最適化アルゴリズムとの比較を行うため、計算回数は64回までとなります。
最適化計算結果について
AIPODのアルゴリズムと他アルゴリズムの最適化計算の結果は下記となります。
ベースライン抵抗係数 | 0.00363 | ||
アルゴリズム | 回数 | 抵抗係数 | 向上率 |
競合 | 31 | 0.003508 | 3.36% |
64 | 0.003508 | 3.36% | |
AIPOD | 24 | 0.003491 | 3.83% |
64 | 0.003448 | 5.01% | |
最終的な結果として、制限された64回最適化計算のでAIPODは5.01%の向上を達成し、競合となる他アルゴリズムは3.36%となりました。
AIPODと他アルゴリズムの最適化プロセスが下記となります。
競合アルゴリズムは、最適化の初期段階では比較的早く性能が向上していきますが、スタミナ不足に陥り、局所的な極地に達してからそれ以上の向上が見られません。
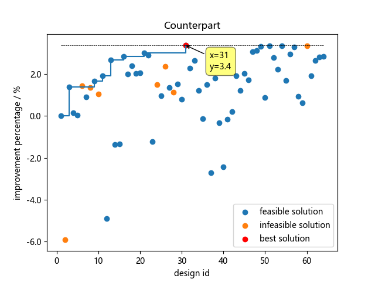 | 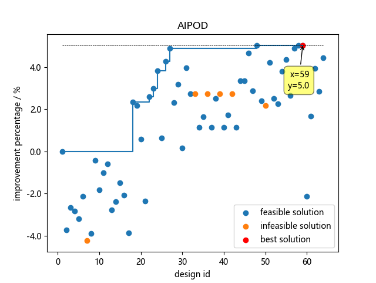 | 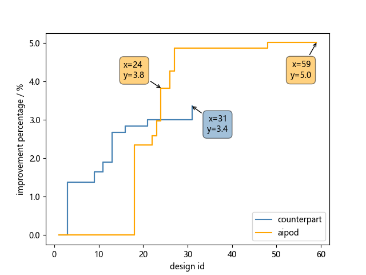 |
| (a)競合アルゴリズム | (b)AIPOD | (c)アルゴリズム履歴比較 |
AIPODの最適化プロセスでは、AIPODの独自機能であるBound-break機能が有効になっています。
この機能は、定義された設計空間の範囲が適切に設定されていない場合に、その範囲を超えた探索を指示する機能であり、不確定な設計空間による最適化効率の低下防止に繋がります。
下記の表より、競合アルゴリズムは設計空間範囲内での探索のみを行っている一方、AIPODのSilverBulletアルゴリズムは、設計空間を超えた計算を行うことで、64回という少ない最適化スケールにおいても、良好なパフォーマンスを発揮していることがわかります。
変数1 | 変数2 | 変数3 | 変数4 | 変数5 | 変数6 | |
範囲 | -0.5~1 | -5~20 | -0.01~0.01 | -0.005~0.005 | -0.03~0.3 | -0.4~0.4 |
競合 | 0.7 | -0.5 | -0.01 | 0.004 | 0.3 | -0.4 |
AIPOD | 1.01 | 10.41 | -0.0097 | 0.0037 | 0.589 | -0.95 |
競合アルゴリズムとAIPODのそれぞれの最適候補となる船体形状が下記となります。
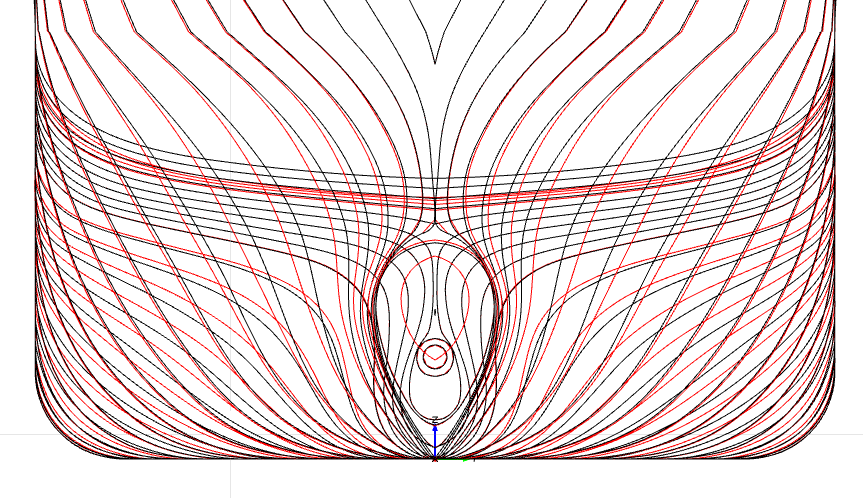 | 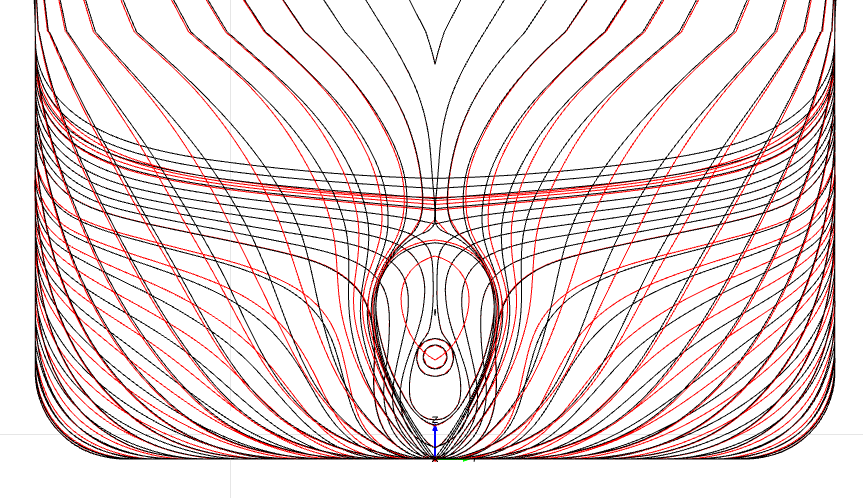 |
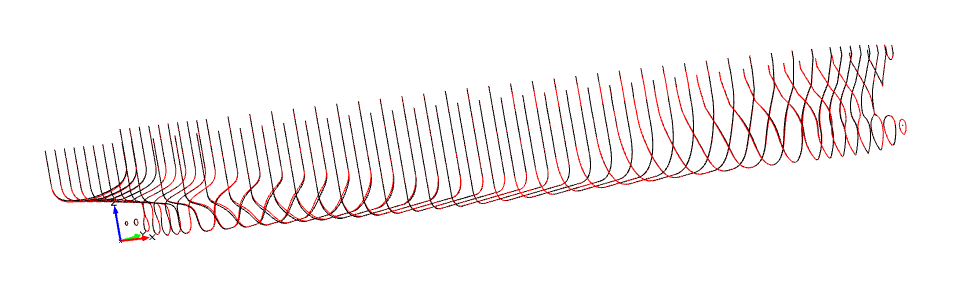 | 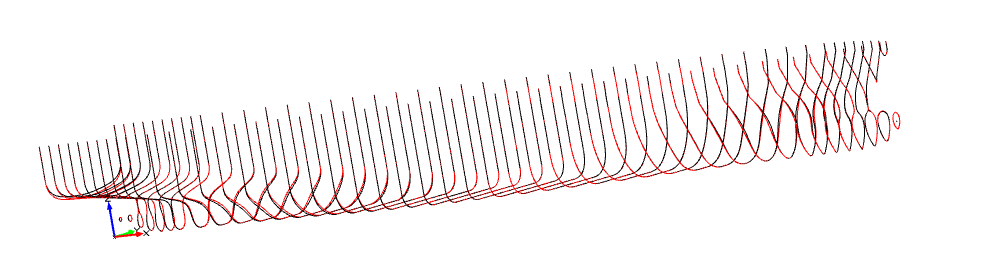 |
| (a)競合アルゴリズム | (b)AIPOD |
