自社開発の最適化プラットフォームであるAIPODによるラムジェットエンジンのエアインテーク最適化についてご紹介します。

本記事は、以下4つの項目で構成されています。

1．CAD＋最適化ソフトウェアCAESESによるパラメトリックモデリング

2．自動シミュレーションプロセスの構築

3．最適化プラットフォームAIPODによる自動最適化

4．エアインテークの性能検

ラムジェットエンジンはマッハ数3以上の吸気設計が対象となり、混合気が流入して出口が亜音速流となる、ジェットエンジンの1種です。

異なる飛行マッハ数に対応するため、スパイクと呼ばれるセンターコーンを前後に移動させることができ、最大飛行マッハ数3.5に達すると、テーパ形状の頂点で形成されるマッハ線はちょうどリップと交差します。

流れ場が軸対称であること、リップ形状が扇状の圧縮面を使用していることを考慮すると、空力関係式の換算では最適な波動配置を取得することは難しくなります。

従って、本ケースではパラメトリックモデリングとシミュレーションによる最適化の組み合わせを採用し、最終的には総圧回復係数に基づいた最適化計算を実行しました。

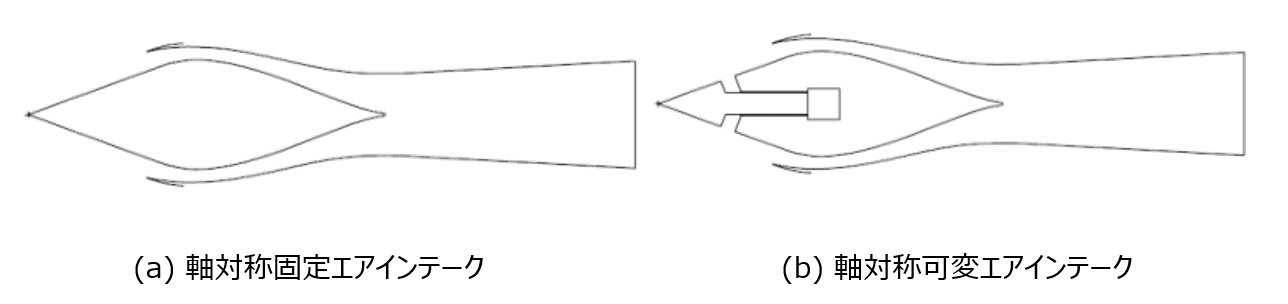
図1: パラメトリックな可変エアインテーク例(参考文献より)

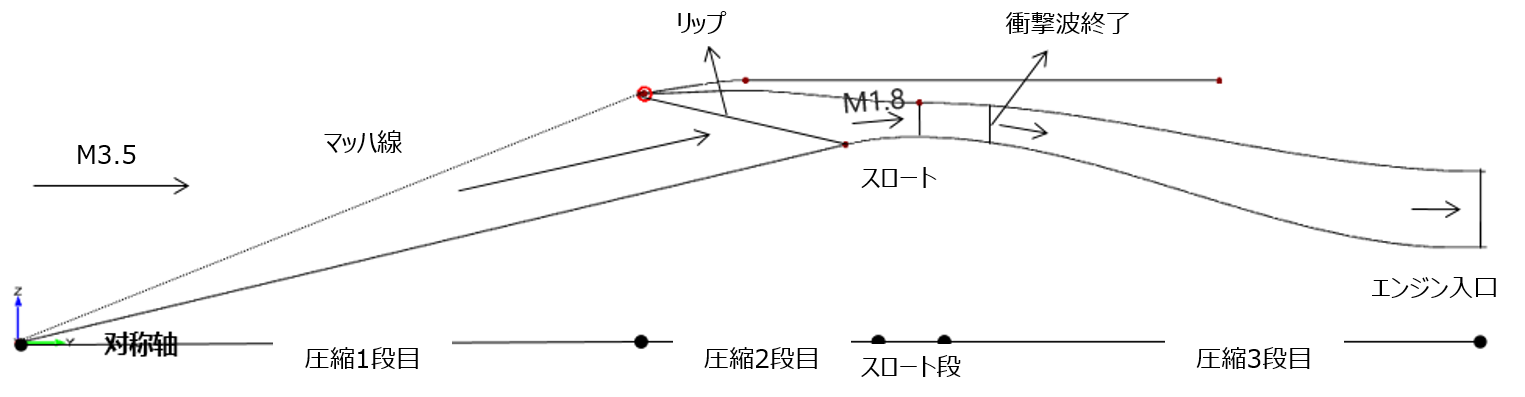
図2: エアインテークの原理

混合気のエアインテークを設計する場合、吸気入口の始動性能を考慮する必要があります。

CFD計算では、スロート面積が小さすぎたり、背圧が高すぎたりすると、指定した流れを引き込めずに逆流が発生して計算が発散します。

そこで、設計の最適化プロセスにおいて、ソリューションの始動性能を検証しました。

吸気入口が正常に始動できるようになると、総排出圧性能はスロート後のサージの位置と密接に関係しており、サージが膨張部のスロートに近いほど、吸気入口の総排出圧は高くなります。

シミュレーションでは、臨界状態に近い最大の出口総圧力性能を得るために、エアインテーク流路の出口における背圧を徐々に増加させる必要があるため、最適化手順は以下の4つのステップに分かれてました; 

ステップ1: CAESESでパラメトリックモデルを作成し、インナーリップ開口部やスロート流路の形状変形をパラメータ制御

ステップ2: パラメトリックモデルのエクスポート、メッシュモデルの自動作成、シミュレーション、結果データのエクスポート、などのプロセスをバッチ形式として自動化

ステップ3: スロート部のマッハ数と全圧を求め、衝撃波の公式換算により波後の全圧を取得、この値を最適化目標としたAIPODの最適化プロセスを構築し、スロート部の最適形状を計算

ステップ4: 最適スロート形状に基づいてディフューザを接続し、背圧を徐々に増加させることによって、エアインテークの全圧性能を取得

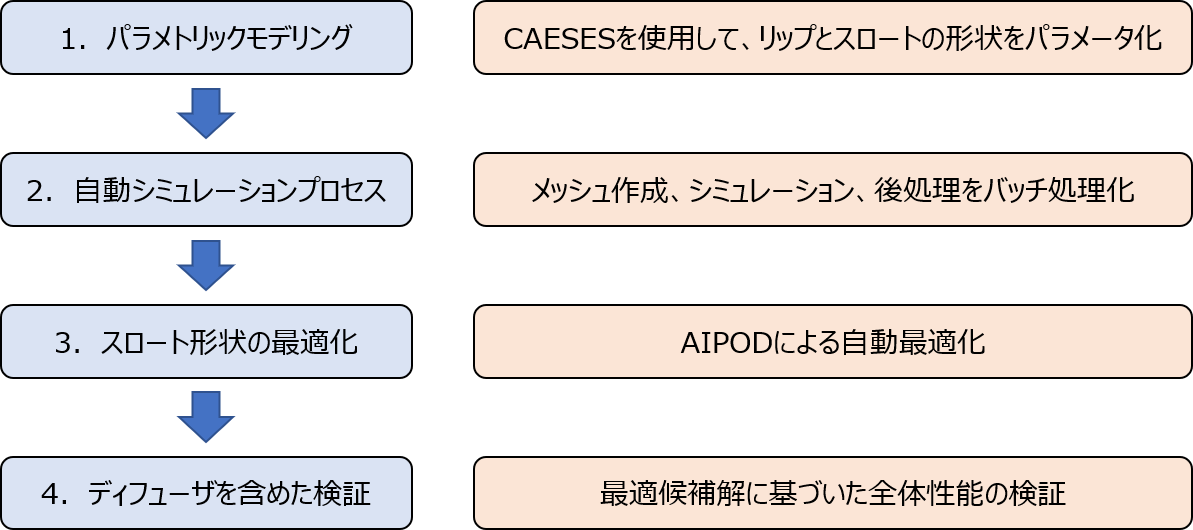
図3: 全体ステップ

ステップ1: CAESESによるパラメトリックモデリング

パラメトリックモデルはエアインテークの形状特徴を生かした軸対称モデリングとなっており、CAESESの各種CAD機能を使用して構築されています。

吸気状態は変化しないため、流路のリップ角とスパイクコーン角は最適化を行わず、設計上の特徴は以下となります; 

(a) 最適化された状態の流入マッハ数はM3.5

(b) スパイクコーン角度は変更せず、スロート部とスパイクコーンの間の移行は、半径がパラメータ化された円を使用

(c) スロートの流路に水平な直線を追加することで、スロート流路の範囲と位置を変化

(d) 前縁部分の後方インナーリップは直線であり、Fsplineカーブでスロート部に接線して、角度と曲率をパラメータ化

(e) スロート部の環状部の高さがパラメトリック

(f) 混合気出口の位置と寸法は変更なし

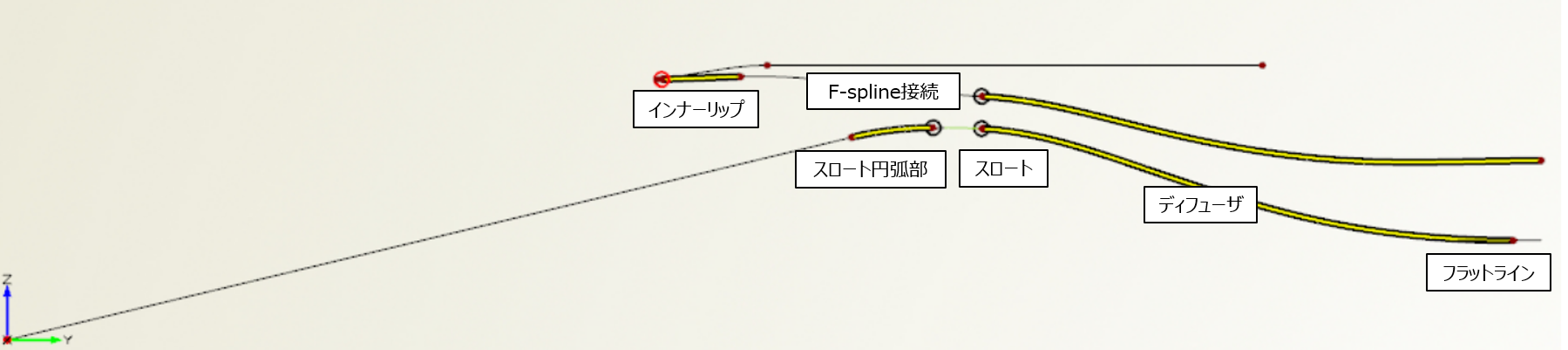
図4: パラメトリックモデリングの構成

ステップ2: 自動シミュレーションプロセスの構築

計算精度を確保するため，本ケースでは構造メッシュを採用しています。

メッシュ数は、スロートが40,000[cells]、 ディフューザが50,000[cells] となっています。

図5: (左)スロートのみ、(右)ディフューザ含む

軸対称エアインテークの空力設計が完了した後、CAESESを使用したパラメトリックモデリングを行い、接続機能を使用してメッシュモデル作成と計算をスクリプトで呼びしてシミュレーションプロセスを自動化しています。

最適化計算プロセスはAIPODで構築されており、CAESESのスクリプト(fscファイル)をバッチモードで呼び出し、パラメータ定義、形状出力、シミュレーション、結果出力などを自動化します。

パラメータ入力機能により、fscファイルを編集し、パラメータをファイルから抽出します。

パラメータ抽出機能では、シミュレーション結果を読み込み、通常の衝撃波式の編集して、最適化目標(波後の全圧回復係数)を取得します。

最後に、最適化アルゴリズムによる自動最適化を実行して、最適スロート形状によるシミュレーション結果を迅速に得ることができます。

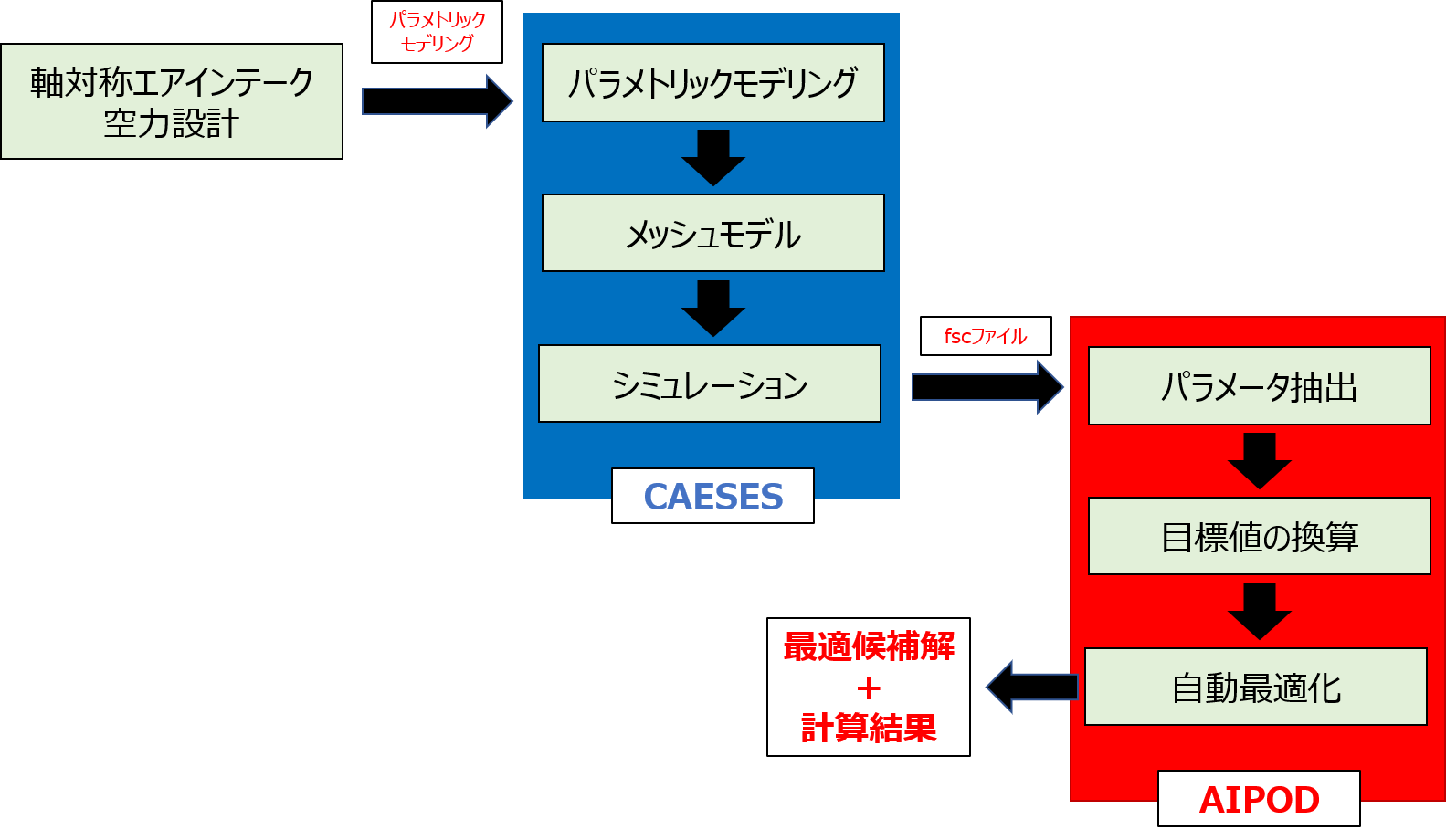
図6: 最適化プロセス

ステップ3: AIPODによる自動最適化

AIPODで最適化を実施する際の運用プロセスを下記に示します。

計算フローの構築、入力ファイルの追加、出力ファイルの追加、変数定義の記述、シミュレーションデータの読み込み、最適化対象の変換、最適化対象の選択、最適化アルゴリズムの選択の合計8つの設定を行いうことで自動最適化プロセスが構築されます。

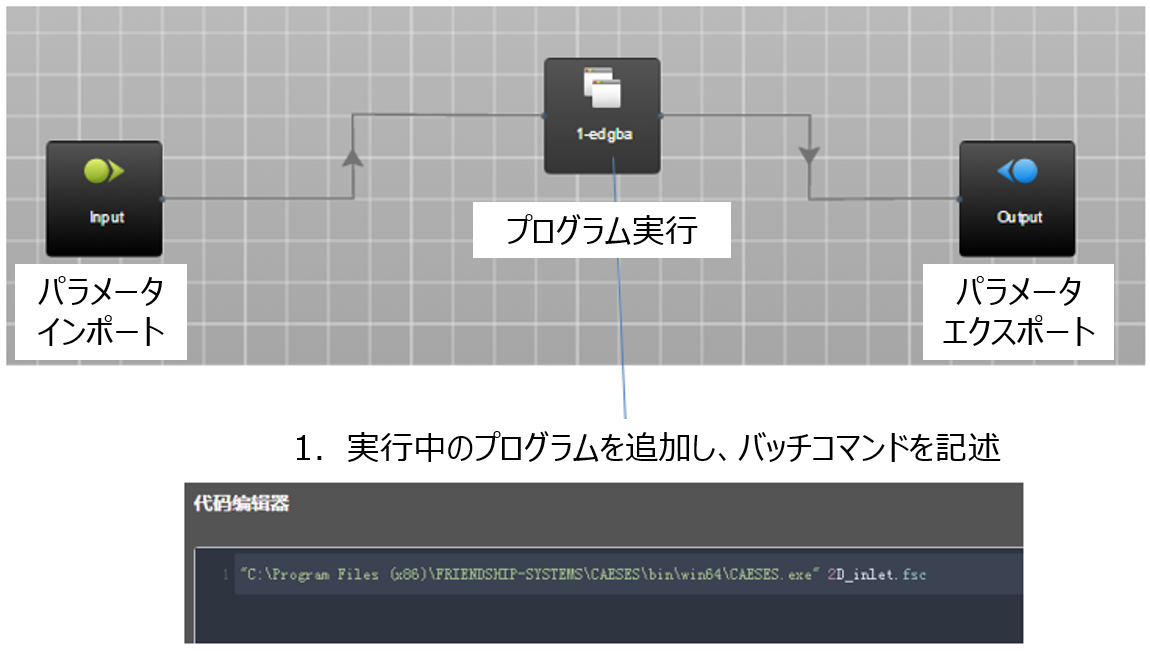
図7: 計算プロセスの構築

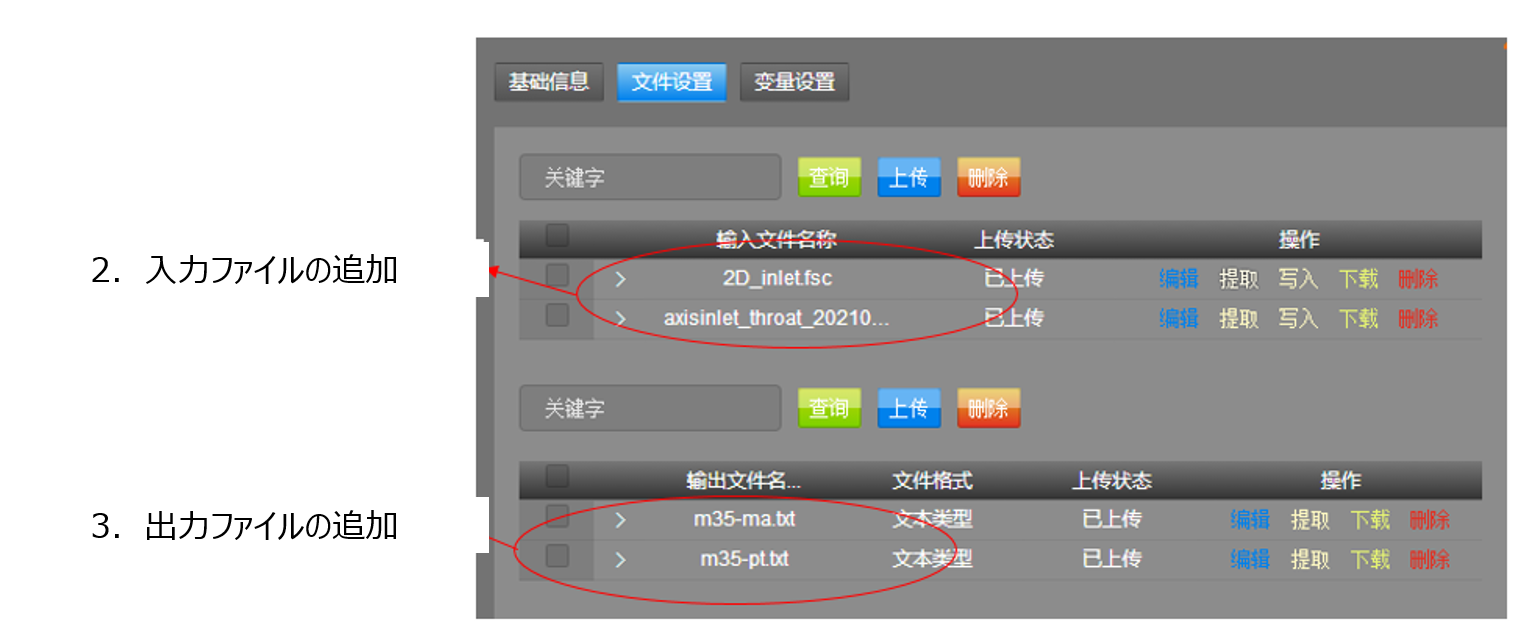
図8: 計算ファイルの追加

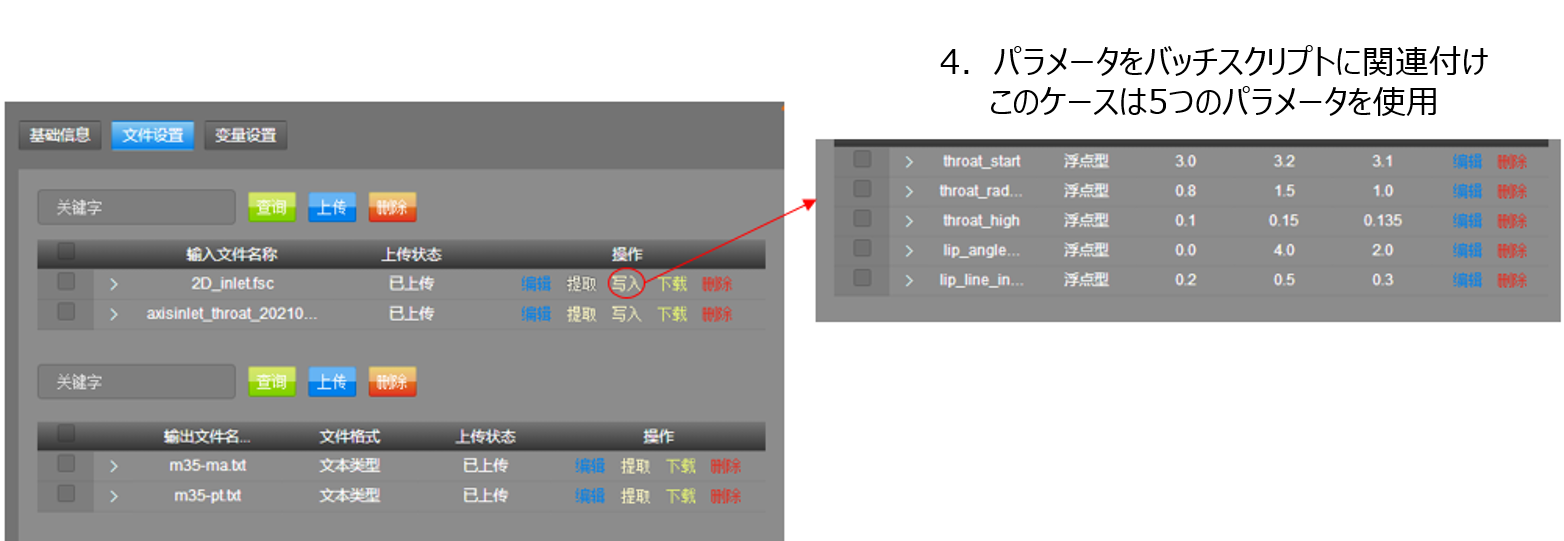
図9: 最適化パラメータの定義

図10: 目標値となる変数作成

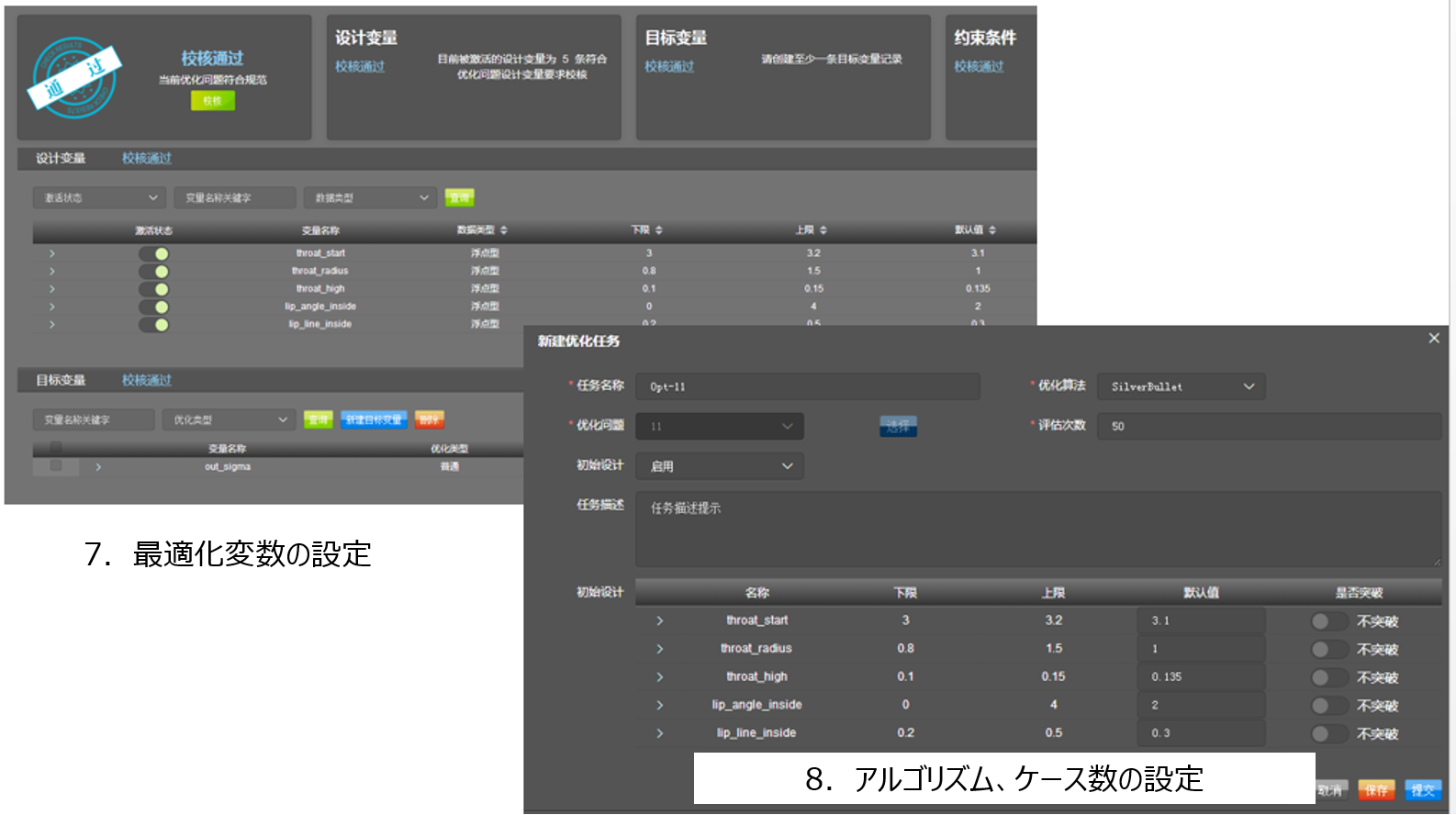
図11: 最適化アルゴリズムの選択

ちなみに、AIPODを使用していない場合のオリジナル最適化計算では、入口マッハ数3.5の状態において、スロート部マッハ数は1.828、サージ後の総圧回復係数は0.697、ディフューザでの最大背圧は200[kpa]、その時点での出口最大総圧回復係数は0.586となっています。

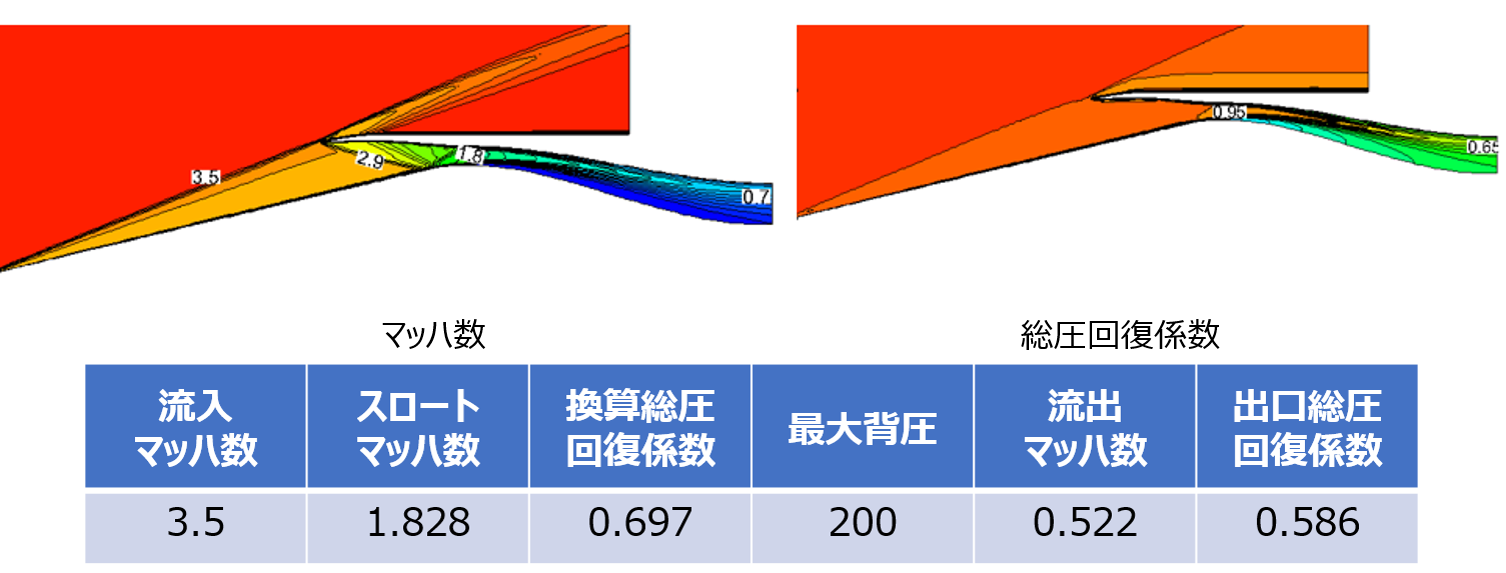
図12: オリジナル最適化結果

AIPODでは、自動最適化探索に独自開発のアルゴリズムである "SilverBullet" を選択し、最適化計算を行います。

効果検証のため、Nelder-Mead Simplexアルゴリズムによる最適化を実施し、最適化結果を比較します。

Nelder-Mead Simplexアルゴリズムは50個の解を取得するように設定し、AIPODのSilverBulletアルゴリズムも50個としました。

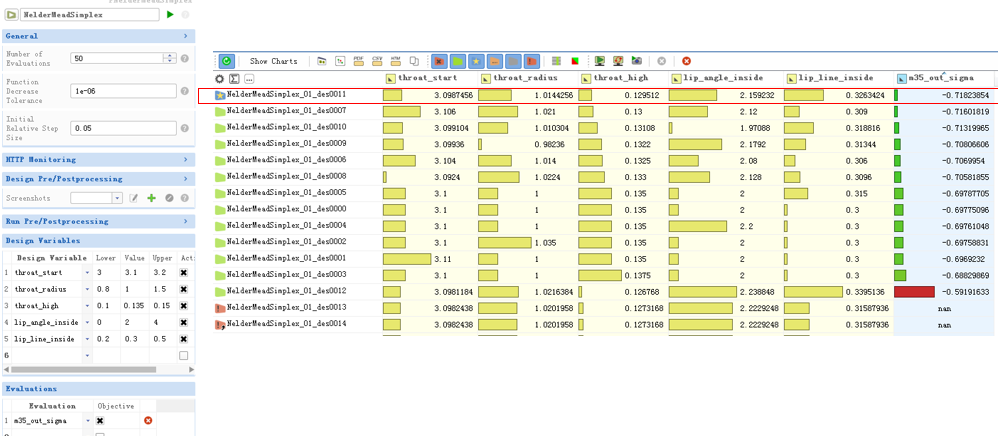
図13:  Nelder-Mead Simplexアルゴリズム

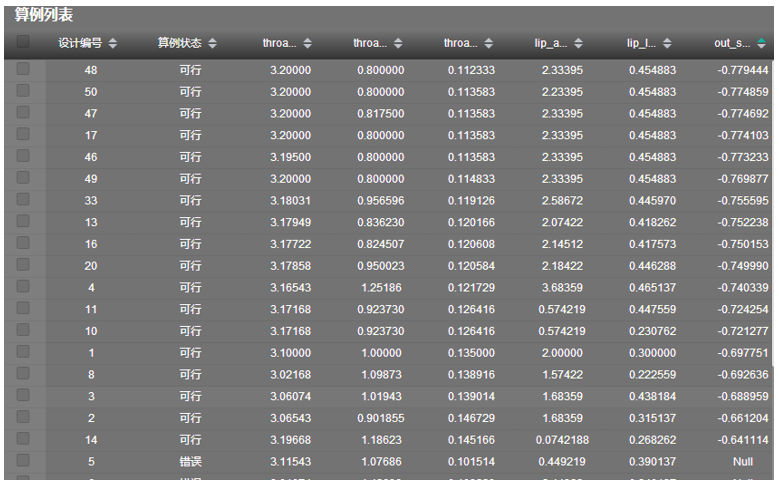
図14: AIPODのSilverBulletアルゴリズム

両者の最適化計算の履歴を見ると、Nelder-Mead Simplexアルゴリズムは、14ケース目で突然停止し、合計12個の有効な結果を取得しました。

一方、SilverBulletアルゴリズムは、50ケースを実行し、17の有効な結果を得ることができました。

比較すると、SilverBulletアルゴリズムは、4ケース目でNelder-Mead Simplexアルゴリズムよりも優れた解を取得し、その間にある無効な解を排除した後、48番目の解が最適であることを示しました。

これは、SilverBulletアルゴリズムが、制約条件下においてもロバストな探索能力を持つことを実証しています。

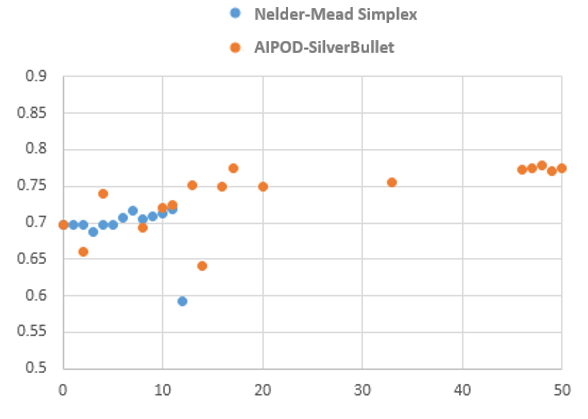
図15: 最適化計算の履歴

エアインテークの性能検証

2つの最適化アルゴリズムで得られたスロート部の最適形状に基づき、ディフューザーを追加し、背圧を徐々に増加させることでエアインテーク全体の性能を取得しました。

オリジナルの最適候補解と比較すると、Nelder-Mead Simplexアルゴリズムでは最高総排出圧が2.7%増加し、SilverBulletアルゴリズムでは12.3%増加しています。

流れ場のコンター図を比較すると、リップとスロート形状の最適化により、入口管路の正常な始動を確保しつつ、スロート部のマッハ数を1.8から1.5に低減することができており、衝撃波による総圧損を低減していることが確認できます。

それと同時に、流れ方向の改善によってディフューザ内側の流れ分離の影響を受ける面積も減少していることが分かりました。

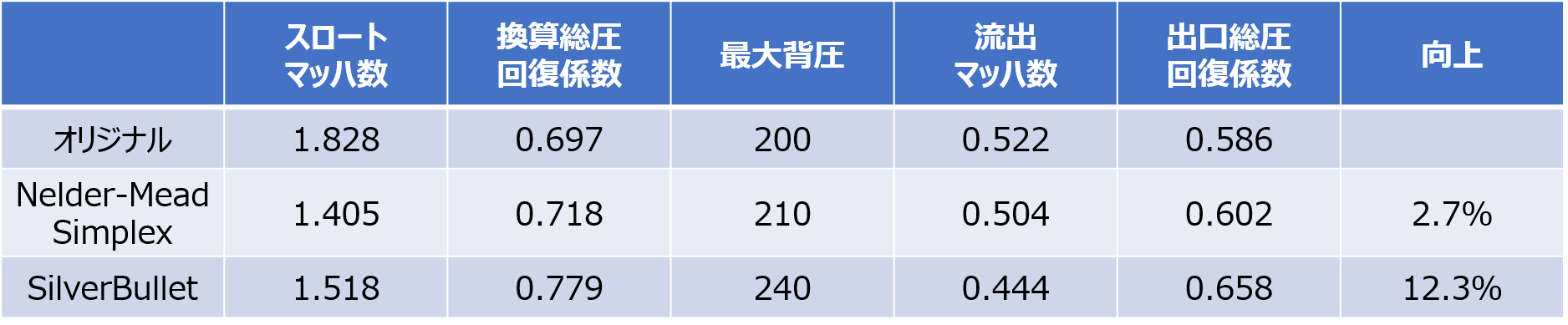
図16: 全体の性能比較

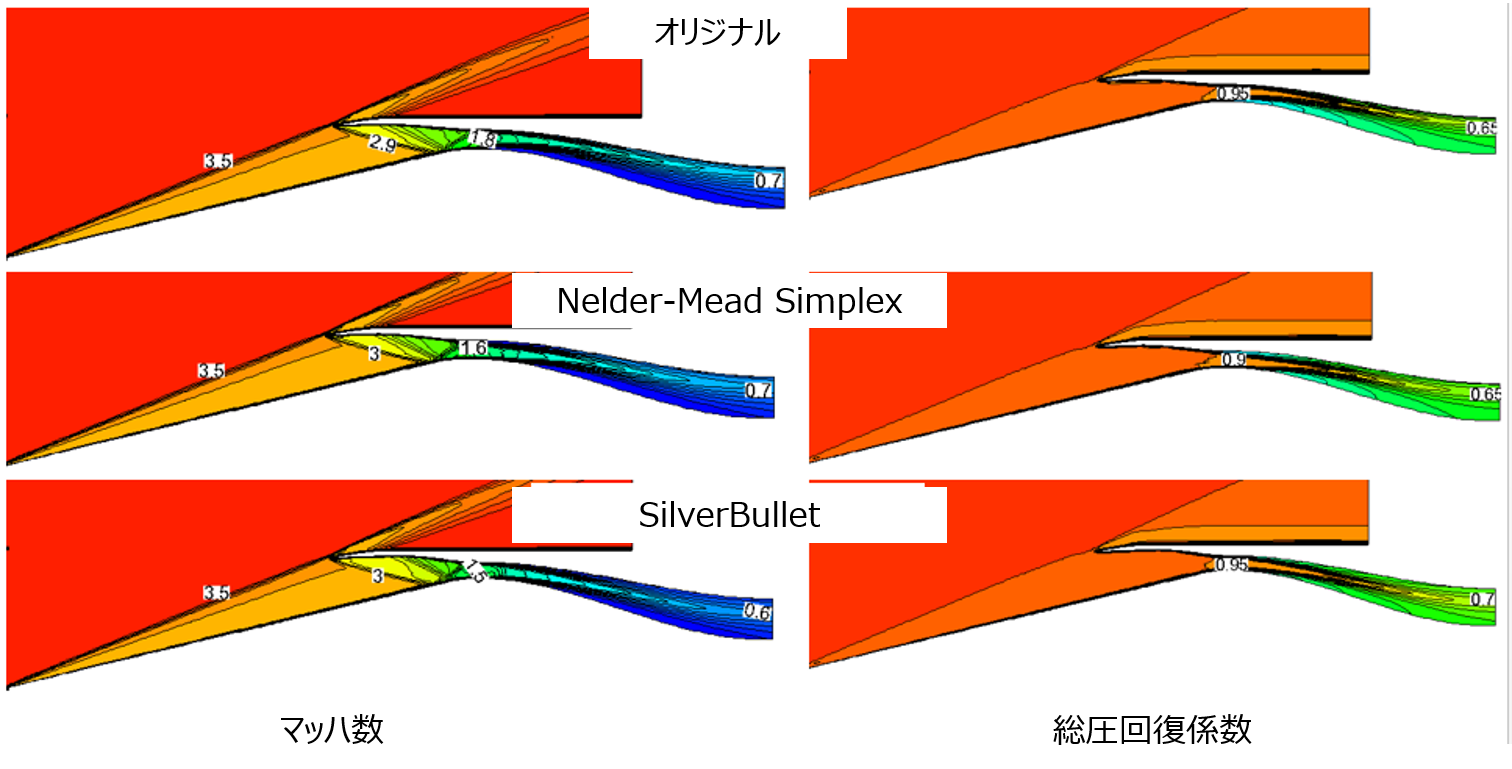
図17: 全体の流れ場

最後に

工業設計のための汎用最適化プラットフォームAIPODは、操作が簡単かつユーザーフレンドリーなインターフェースを備えています。

搭載された自社アルゴリズムSilverBulletは、インテリジェントサンプリング技術、連成最適化技術、コアセットのパラメータ指標を統合し、全体最適化と局所探索を動的に調整し、小さな計算スケールで効率的に最適化性能向上を達成します。

今回の適用ケースにおいて、SilverBulletは50の計算を確実に実行し、工業分野における複雑なシミュレーション最適化に適した探索機能を実現しました。

AIPODソフトウェアには、エージェントモデルのトレーニングやエージェント最適化などの機能も備わっています。

最適化ソフトウェアにご興味のある方は、弊社までお問い合わせください。

参考文献; 

1. 滕健，袁化成，轴对称变几何进气道初步研究，中国力学大会，2011.

2. 梁德旺，袁化成，张晓嘉，影响高超声速进气道起动能力的因素，宇航学报，2006.

3. 袁化成，梁德旺，高超声速进气道再起动特征分析，推进技术，2006.